Examples & Pricing

System of Nonlinear Equations

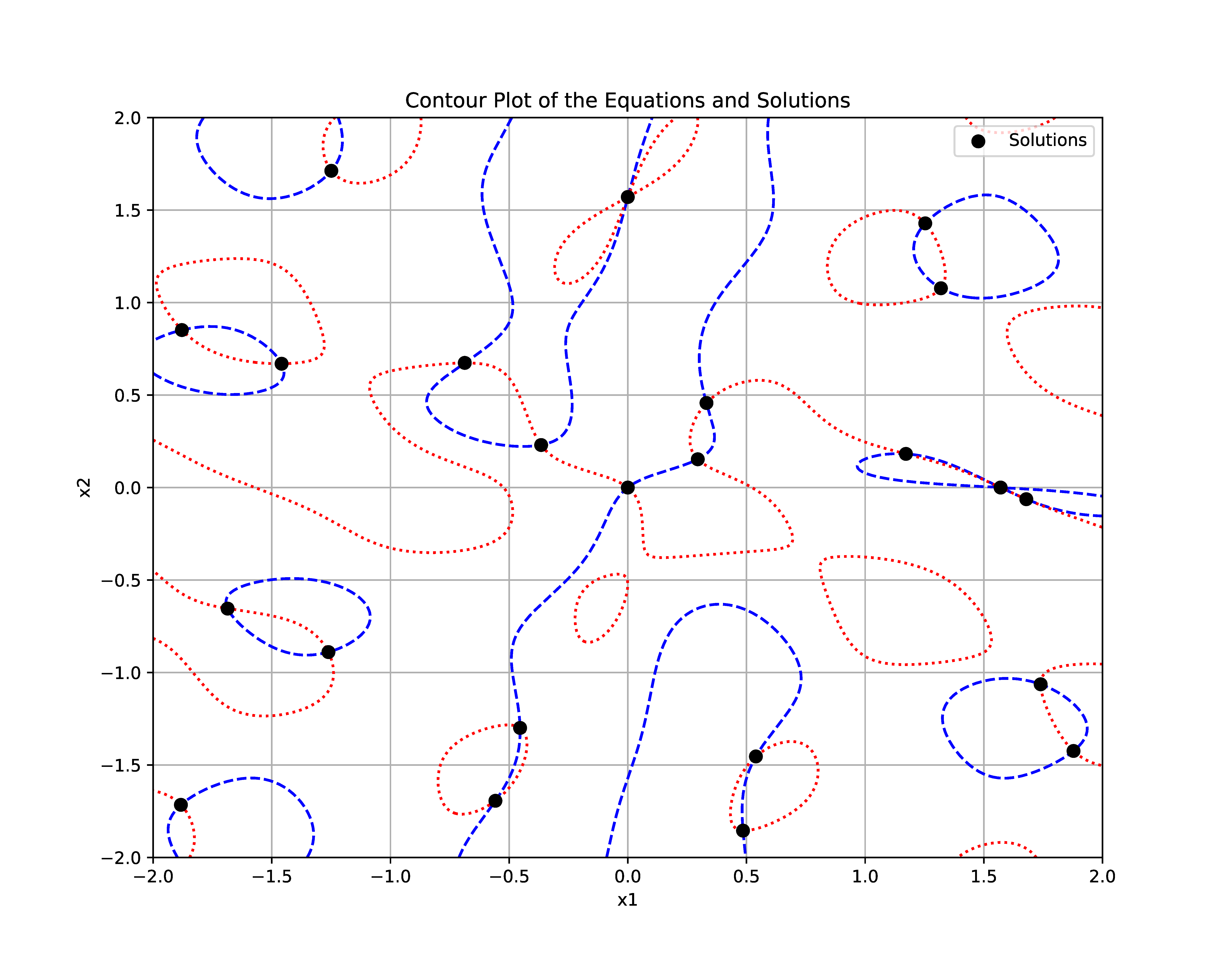
In this example, consider a system of nonlinear equations (SNE) defined by two transcendental equations in two unknowns. The problem is defined by the following equations:

• Blue Contour:

  $f_1(x_1, x_2) = x_1 - x_1 \sin(x_1 + 5x_2) - x_2 \cos(5x_1 - x_2) = 0$

• Red Contour:

  $f_2(x_1, x_2) = x_2 - x_2 \sin(5x_1 - 3x_2) + x_1 \cos(3x_1 + 5x_2) = 0$

The solutions to this SNE are the points of intersection between the blue and red contours. Identifying all such points within a specified region is non-trivial due to the complexity and nature of the equations. There are 23 distinct solutions to the SNE shown in the image below which exist within the region

$x_1,x_2\in [-2,2]$

---

Pricing & Solver Metrics

Metrics based on different starting points: 20, 40, 60, 80, and 100. A total of 500 independent runs were performed. The selection of starting points was done randomly. The Nelder-Mead local search algorithm was utilized for the process. (See the code below)

Javascript

const TOXEUS_EMAIL = ""
const TOXEUS_PASSWORD = ""


const { Client, Model } = require('toxeus-node-sdk');
const toxeus = new Client(TOXEUS_EMAIL, TOXEUS_PASSWORD);

const model = new Model();

// Beginning of Solver Parameters:

// (optional) Set the algorithm parameters (default: {"algorithm": "Nelder-Mead"})
model.setAlgorithmParameters({"algorithm": "Nelder-Mead"})

// (optional) Set the number of starting points the solver should search from in parallel (default: 1, max: 100)
model.setNumberOfStartingPoints(20);

// (optional) Set the maximum acceptable error of solutions that the solver will return (default: 10)
model.setMaximumAcceptableError(0.00001);

// (optional) Set the minimum acceptable distance between distinct solutions that the solver will return (default: 0.01)
model.setMinimumAcceptableDistanceBetweenDistinctSolutions(0.001);

// (optional) Set the maximum number of solutions that the solver will return (default: infinity)
model.setMaximumNumberOfSolutionsToReturn(1000);

// (optional) Set the maximum solver runtime in seconds (default: 900)
model.setMaximumSolverRuntimeInSeconds(60);

// (required) Define a new decision variable with a name, lower bound, upper bound, and initial region to select starting points from
model.addDecisionVariable({
     name: "x_1",
     lower_bound: -2,
     upper_bound: 2,
     initial_region_to_select_starting_points_from: {
          lower_bound: -2,
          upper_bound: 2
     }
});

model.addDecisionVariable({
     name: "x_2",
     lower_bound: -2,
     upper_bound: 2,
     initial_region_to_select_starting_points_from: {
          lower_bound: -2,
          upper_bound: 2
     }
});

// (required if no objective is set) Define a new constraint with an expression and optionally, a name
model.addConstraint("0 = x_1 - x_1 * sin(x_1 + 5*x_2) - x_2 * cos(5*x_1 - x_2)");
model.addConstraint("0 = x_2 - x_2 * sin(5*x_1 - 3*x_2) + x_1 * cos(3*x_1 + 5*x_2)");


model.setNumberOfRuns(1);

// End of Solver Parameters

// Solve the model and save the results to a JSON file
toxeus.Solve(model);

Metric
Number of Starting Points	$20$	$40$	$60$	$80$	$100$
Average Total Runtime	$0.369\,\text{s}$	$0.510\,\text{s}$	$0.673\,\text{s}$	$0.811\,\text{s}$	$0.954\,\text{s}$
Average Number of Solutions Found	$10.928$	$15.848$	$18.454$	$19.992$	$21.01$
Average Percent of Solutions Found	$47.51\%$	$68.90\%$	$80.23\%$	$86.92\%$	$91.35\%$
Average Total Gigabyte Seconds Used by Solver	$551$	$664$	$1012$	$1034$	$1488$
Average Cost ($0.005 per Gigabyte Second)	$2.76	$3.32	$5.05	$5.17	$7.44